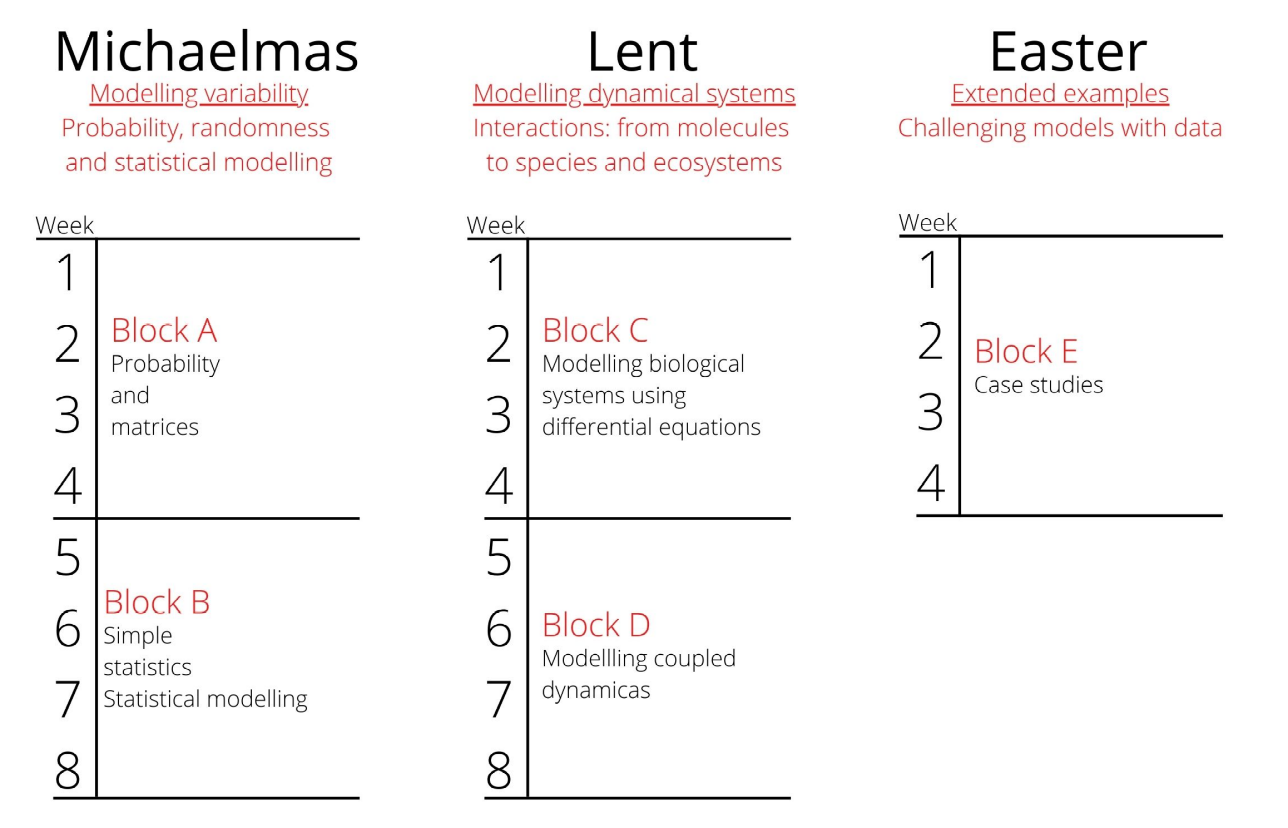
Block A: Probability and Matrices
Part 1 introduces concepts in probability, starting with how probabilities of single and multiple events are defined and ideas of independence and dependence. Key to many probability calculations is the mathematics of counting, or combinatorics, which enables us to enumerate the number of ways in which an event may occur. The lectures also introduce probability distributions, including certain special distributions used to represent random processes in the real world. These enable us to model biological phenomena and make inferences about the factors involved in an experiment. Part 2 concerns mathematical objects called matrices and how to carry out calculations involving them. Matrices are used widely, and a particularly important application involves situations in which a random process moves probabilistically between a finite number of discrete states. We concentrate on cases where transitions between states occur in discrete time (e.g. once per second, per year or per generation). We study the algebra of matrices as far as eigenvalues and eigenvectors, which enable us to evaluate the result when a matrix is repeatedly applied to a vector.
Block B: Statistics and Statistical Modelling
These lectures cover a broad range of statistical techniques used by biologists to analyse data. We will discuss how to formalise biological questions into statistical hypotheses that can be formally tested. We will start with simpler tests, such as t-tests and χ2, and progress to explore linear models that allow us to account for multiple predictors simultaneously. Besides understanding the logic and mechanics of tests, we will focus on how to test whether the assumptions of each test are met, and how to proceed in the – surprisingly common – situations when they are not. The lectures will use output from the statistical language R, providing the theoretical background to correctly interpret the outcome of different analyses when used in real life.
Online material: Introduction to Basic Calculus
These lectures introduce the basic principles of calculus, which is helpful for predicting how biological systems can change over time or over other variables, such as distance. Their purpose is solely to provide those who have not studied mathematics at the post-16 level with the concepts they need to handle the material covered in Block C in Lent term.
The lectures start with an introduction to differentiation, providing a useful way to think about rates of change and why curves are curved. This area has several useful applications, including how to sketch the shape of an unknown function, how to make approximations and how to handle experimental errors. Next comes an introduction to integration, an operation that in effect undoes the consequences of differentiation and enables the area under a curve to be calculated. The final section explains what differential equations are, how they can be used to model biological phenomena such as changes in population, how simple examples can be solved, and the importance of boundary conditions for obtaining a unique solution.
Block C: Modelling using Differential Equations
These lectures show how a range of biological phenomena can be modelled using differential equations, focusing on cases in which the value of a single state variable is changing continuously in time. Examples are largely drawn from population dynamics, although the techniques are relevant much more broadly (see Blocks D and E). The main mathematical skill is solving differential equations via separation of variables. However, qualitative analyses – finding model equilibria and examining long-term stability, as well as using the direction field to sketch solution curves – can often be equally revealing. Such methods can be particularly useful since they allow more complex systems to be investigated without any significant additional conceptual difficulty. These methods also generalise more readily to situations in which the value of multiple state variables are changing in time in a coupled way, for example chemical reactions involving multiple chemical species (see Block E), or ecological interactions involving more than one biological species with population sizes that depend on each other (see Block D).
Block D: Modelling Coupled Dynamics
These lectures extend the mathematical methods covered in Block C to allow analysis of more complicated biological models (in particular the dynamics of populations that are coupled together). The main focus is an examination of the dynamics of linear and non-linear coupled differential equations, both analytically and by graphical "phase plane" techniques. In the second half of Block D we use these methods to look at various coupled population systems, including predator-prey systems, competition within and between species, and the mathematical modelling of epidemics in plants, humans and animals.
Block E: Case Studies
Part 1 looks at models of animal behaviour that are based on the idea of selection as a fitness-maximising process. Beginning with straightforward applications of optimality, we move on to the concept of evolutionary stability and simple game theoretical models of social behaviour, focusing in particular on the evolution of parental care as an illustrative case. Part 2 makes use of some of the mathematical tools discussed in Lent term to gain insight into a range of widely applicable chemical and biochemical processes, from radioactive decay, to reactions catalysed by enzymes and metabolic reaction networks. Part 3 introduces methods for the analysis of biological sequence data. The lectures will discuss existing software and online databases, with an overview of underlying theory where appropriate.